LaTeX-Manual-Sekundarstufe2: Unterschied zwischen den Versionen
Aus Augenbit
| Zeile 83: | Zeile 83: | ||
|Vektor y ist gleich Spaltenvektor 1 2 3 Vektorende | |Vektor y ist gleich Spaltenvektor 1 2 3 Vektorende | ||
|<code>\vec{y} = \mat{1 \\ 2 \\ 3} </code> | |<code>\vec{y} = \mat{1 \\ 2 \\ 3} </code> | ||
|[[LaTeX-Manual-Sekundarstufe2#Anmerkung|Anmerkung 1]] | |[[LaTeX-Manual-Sekundarstufe2#Anmerkung|Anmerkung 1)]] | ||
|- | |- | ||
|[[Bild:Matrix.gif]] | |[[Bild:Matrix.gif]] | ||
Version vom 27. Januar 2010, 11:54 Uhr
Analysis
| Schwarzschrift | Prosa | LaTeX | ... |
|---|---|---|---|
| [math]\displaystyle{ n \to \infty }[/math] | n geht gegen unendlich | n \to \infty
|
|
| [math]\displaystyle{ \lim_{h \to 0} }[/math] | Limes h gegen 0 | \lim_{h \to 0}
|
|
| [math]\displaystyle{ \lim_{x \to x_0} }[/math] | Limes x gegen x Index 0 | \lim_{x \to x_0}
|
|
| [math]\displaystyle{ f\ ' (x), f\ ''(x) }[/math] | f Strich von x, f zwei Strich von x | f'(x), f''(x)
|
|
| [math]\displaystyle{ \sum_{i=0}^n A_n }[/math] | Summe von i gleich 0 bis n über A Index n | \sum_{i=0}^n A_n
|
|
| [math]\displaystyle{ \int_a^b f(x) dx }[/math] | Integral von a bis b über f von x dx | \int_a^b f(x) dx
|
Stochastik
| Schwarzschrift | Prosa | LaTeX | ... |
|---|---|---|---|
| [math]\displaystyle{ n! }[/math] | n Fakultät | n!
|
|
| [math]\displaystyle{ {n \choose k} }[/math] | Binomialkoeffizient n über k | {n \choose k}
|
|
| [math]\displaystyle{ \sigma \qquad \Omega }[/math] | klein Sigma groß Omega | \sigma \Omega
|
Analytische Geometrie
| Schwarzschrift | Prosa | LaTeX | ... |
|---|---|---|---|
| [math]\displaystyle{ \vec{x} = (x \; y \; z) }[/math] | Vektor x ist gleich Zeilenvektor x y z Vektorende | \vec{x} = (x \; y \; z)
|
\vec{x} = (x & y & z) oder \vec{x} =(x ; y ; z)
|
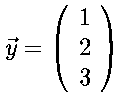
|
Vektor y ist gleich Spaltenvektor 1 2 3 Vektorende | \vec{y} = \mat{1 \\ 2 \\ 3}
|
Anmerkung 1) |
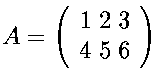
|
Matrix groß A ist gleich Zeilenanfang 1 2 3 Zeilenende Zeilenanfang 4 5 6 Zeilenende Matrixende | A = \mat{ 1 \; 2 \; 3 \\ 4 \; 5 \; 6 }
|
A = \mat{ 1 & 2 & 3 \\ 4 & 5 & 6 }
|
Anmerkungen
Anmerkung 1)
Diese Kurzschreibweise stammt aus der "Dresdener Abkürzungsliste" von U. Nitsch. Beim Übersetzen wird diese mit der Datei vorspann.tex automatisch eingebunden. Spaltenvektoren werden hier als Matrizen mit einer Spalte betrachtet.